Poker Hands 5 Of A Kind

admin

Poker is all about making the best five-card poker hand from the seven cards available (five community cards plus your own two hole cards). That means in the event of a tie with four of a kind, three of a kind, two pair, one pair, or high card, a side card, or 'kicker', comes into play to decide who wins the pot. Each of these poker hands was evaluated for matched ranks (pairs, 3 of a kind, etc.), straights, and flushes. Wild cards introduce multiple evaluations for a given hand, and the best standard evaluation for any given hand is used in the tables. Data from this page may be freely used provided it includes an acknowledgement to the author. The number of different 5 -card poker hands is. 52 C 5 = 2,598,960. A wonderful exercise involves having students verify probabilities that appear in books relating to gambling. For instance, in Probabilities in Everyday Life, by John D. McGervey, one finds many interesting tables containing probabilities for poker and other games of chance. Is4s( Card h ): detects whether the Poker hand h contains a Four of a Kind; isFullHouse( Card h ): detects whether the Poker hand h contains a Full House; is3s( Card h ): detects whether the Poker hand h contains a Three of a Kind. Poker hands from highest to lowest 1. Four of a kind All four cards of the same rank. Full house Three of a kind with a pair. Flush Any five cards of the same suit, but not.

by Cactus Kev

The distribution of all possible 5-card poker hands is well known.With a standard deck of 52 cards, there are C(52,5), or 2,598,960 ways toselect five distinct cards (where order does not matter). If wedetermine the hand value for each of those approximately 2.6 million poker hands,we get the following table:

Five Card Poker Hands
40Straight Flush
624Four of a Kind
3,744Full House
5,108Flush
10,200Straight
54,912Three of a Kind
123,552Two Pair
1,098,240One Pair
1,302,540High Card
2,598,960TOTAL

It is this table that initially gave us our poker hand rankings.Notice that the fewer the ways available to make a particular pokerhand, the higher its value. That's why a Straight Flush beatsa Four-of-a-Kind. There are only 40 ways to make a Straight Flush,but 624 ways to make a Four-of-a-Kind. I have sometimes seen the abovetable given where a Royal Flush is listed separately, and rankeddirectly above a Straight Flush. In my opinion, this is unnecessary,since a Royal Flush is simply a special case of a Straight Flush (itjust happens to be the highest Straight Flush possible). We don'tsingle out Four Aces with a King kicker as being the highest possibleFour-of-a-Kind hand, so there is no need to single out the RoyalFlush hand either. But some tables list it that way, so just beaware that I've have combined the Royals with the other Straight Flushes.

Now, recently I got to thinking about wild card games, and I wonderedwhat the frequency table looked like when you counted Deuces as beingwild. Since the rules for wild card games are numerous and definatelynot standardized, I used the following stipulations:

  1. Five-of-a-Kind hands are allowed.
  2. Wild cards can represent any card (no restrictions).
  3. If a hand contains one or more wild cards, that hand's value is the highest possible it can be.
  4. Double-Ace and Triple-Ace Flushes are not allowed.
Rule 1 is included because most players like to have Five-of-a-Kindhands when playing with wild cards. Rule 2 means that a wild cardcan be anything -- it is not restricted in its value like the Jokeris in some games (i.e. can only be used as an Ace, or to completea Flush or Straight). Rule 3 is required because handswith wild cards can have multiple values. For example, if you holdtwo Kings, two wild Deuces, and a Jack, you can claim you have thefollowing five hands:
  • Four of a Kind (KKKKJ)
  • Full House (KKKJJ or JJJKK)
  • Three of a Kind (KKKJx)
  • Two Pair (KKJJx, AAKKJ, etc.)
  • One Pair (KKJxx)
Since the highest hand wins in most poker games, it makes sense to countwild card hands as their highest possible value. So in the above example,that hand would be counted as a Four-of-a-Kind. Rule 4 is included sothat a hand like A983 (all Spades) with a wild Deuce will be counted asan AK983 Flush, and not an AA983 Flush (a double Ace-High Flush, whichis allowed in some home games).

My first thought was to search the internet and check poker books tosee if such a table already existed. The internet turned up nothing,but the book 'Scarne's Guide to Modern Poker' had the table I was looking for.However, I never take such tables as gospel, and I wanted to computeand verify the values myself (which is a good thing, as I soon learnedthat Scarne's table was incorrect!) I also posted this question inthe rec.gambling.poker newsgroup, and a number of RPG'ers postedresults they had either found or computed. Even then, some of thefigures given were incorrect or inconsistant; so I decided to determinethe hand frequencies myself.

There were a couple of ways I could tackle this problem. One way would beto use math theory and combinatorics to enumerate all the hand rank frequencies.Another would be to write some poker code to loop over all 2,598,960 possiblefive card poker hands, and determine each hand's value if Deuces were wild.I decided to do both, since I should get the same results using either method,and it would act as a sanity check.

I had already written some 'C' code that determined the value of a specificfive card poker hand. It required just a little massaging to get it towork with Deuces being wild. After lots of debugging and code checking,I finally obtained the following results:

Poker Hand Frequencies
with Deuces Wild
672Five of a Kind
2,552Straight Flush
31,552Four of a Kind
12,672Full House
14,472Flush
62,232Straight
355,080Three of a Kind
95,040Two Pair
1,225,008One Pair
799,680High Card
2,598,960TOTAL

Now the question was whether or not these figures were correct. AlthoughI was fairly certain my code was correct, I'd been burned before by makinginvalid assumptions in my coding logic. This meant to be absolutely sure,I needed to validate my results by using math and combinatorics.

Before we start, a quick note about combinatorics. There are oftenmultiple ways to obtain the same answer. In the tables given below,I will give the combinatoric method I used to obtain my answer. You,however, may come up with a completely different way to compute the sameanswer. That is okay. It all depends on how you 'count' your objects.For example, let's say we remove all four Deuces from the deck, and wewish to figure out how many ways we can select five cards of differingranks. One person might look at the problem this way:
There are 48 cards to choose from for our first card. Let's say weselect the King of Spades. For our next card, we only have 44 to choosefrom (because we can't select another King). We select the Six of Diamonds.For the third card, we only have 40 to choose from (because we can'tselect any Kings or Sixes), and so on. So selecting all five cardsgives us 48 x 44 x 40 x 36 x 32 possible permutations.However, we don't care about the order -- we want combinations instead.In order to remove all duplicates, we must divide by 5!(that's 5 factorial, i.e. 5x4x3x2x1). This gives a finalanswer of 811,008.
Now, a second person might come along and reason as thus:
Okay, there are twelve ranks to choose from since the Deuces havebeen removed. I need to choose five ranks out of the possible twelve,so that's C(12,5), or 792 combinations. Now that I have chosen myfive distinct ranks, each of those five cards can be one of fourpossible suits. So I need to multiply 792 by 45. This givesa final answer of 811,008.
See? Two different ways to tackle the problem, but they both come upwith the same result.

Okay, enough talk. Let's start enumerating.First off, I determined how many five card poker hands contained zero Deuces,one Deuce, two Deuces, three Deuces, or all four Deuces. Combinatorics madethis very easy, and the following table shows the results:

Breakdown of Deuce Counts
48hands with four DeucesC(4,4) x C(48,1)
4,512hands with three DeucesC(4,3) x C(48,2)
103,776hands with two DeucesC(4,2) x C(48,3)
778,320hands with one DeuceC(4,1) x C(48,4)
1,712,304hands with zero DeucesC(4,0) x C(48,5)
2,598,960TOTAL

Next, I tackled each of the five possibilities shown above. The first casewas easy. If you have all four Deuces in your five card poker hand, thenyou obviously have a Five-of-a-Kind. So out of the 48 possible hands thatcontain four Deuces, all of them are Five-of-a-Kinds.

Hands with Four Deuces
48Five of a KindC(48,1)
48TOTAL

Next, I took a look at the hands with three Deuces. After some thought,you should realize that if you hold three Deuces, then theabsolute minimum hand you could hold is Four-of-a-Kind.If the other two non-wild cards happen to be a pair, then you have aFive-of-a-Kind. If they are the same suit and close enough in rank, youhave a Straight Flush. Otherwise, you must have a Four-of-a-Kind.No other hands are possible with three wild Deuces.Since there are four Deuces in a deck, but we only need to choose three ofthem, each of the counts will have a factor of C(4,3) for the variouscombinations of three Deuces. For Five-of-a-Kind hands, there are 12ranks to select from (Ace through Trey) for the pair, and C(4,2) waysto form that pair once the rank has been selected. That gives us288 Five-of-a-Kind hands. Straight Flush hands are more tricky to compute. We must enumerate all ways to form aStraight Flush using two non-wild cards. It turns out there are 41 suchways, as shown in the table below. Note that when Deuces are wild,Six-High Straight Flushes are verboten since one can always make a higherStraight Flush.

Straight Flushes with Three Deuces (41 ways)
Royal FlushAK222AQ222AJ222AT222KQ222
KJ222KT222QJ222QT222JT222
King-High Straight FlushK9222Q9222J9222T9222
Queen-High Straight FlushQ8222J8222T822298222
Jack-High Straight FlushJ7222T72229722287222
Ten-High Straight FlushT6222962228622276222
Nine-High Straight Flush95222852227522265222
Eight-High Straight Flush84222742226422254222
Seven-High Straight Flush73222632225322243222
Five-High Straight Flush5A2224A2223A222

With that table, I can now calculate how many Three Deuce Straight Flushhands there are. There are C(4,3) ways to choose three of the four Deuces,times 41 ways to make a Straight Flush, times 4 different suits, givinga total of 656. Once I've eliminated all Five-of-a-Kind and Straight Flushhands, only Four-of-a-Kind are left remaining. I now know the totalsfor hands with three Deuces.

Hands with Three Deuces
288Five of a KindC(4,3) x 12 x C(4,2)
656Straight FlushC(4,3) x 41 x 4
3,568Four of a Kind4,512 - 288 - 656
4,512TOTAL

Next, I worked on the hands containing two Deuces. Note that when holdingtwo wild Deuces, the minimum hand possible is Three-of-a-Kind. Also observethat it is impossible to have a Full House when holding two wild cards.The combinatorics used to calculate the hand frequencies are similar to howwe computed them for the three Deuce hands. It turns out there are 55 waysto make a Straight Flush this time (rather than 41 as before). For Flushhands, we select any three cards (except the Deuce) of the same suit, butthen subtract off the Straight Flush hands since those would be included.For Straights, we use the same 55 ways to make Straight Flushes, but thistime we make sure the suits don't all match. Three-of-a-Kinds would bea real bear to compute, so we take the easy way out. Once we've computedall the other hand frequencies, anything left remaining has to be aThree-of-a-Kind.

Straight Flushes with Two Deuces (55 ways)
Royal FlushAKQ22AKJ22AKT22AQJ22AQT22
AJT22KQJ22KQT22KJT22QJT22
King-High Straight FlushKQ922KJ922KT922QJ922QT922JT922
Queen-High Straight FlushQJ822QT822Q9822JT822J9822T9822
Jack-High Straight FlushJT722J9722J8722T9722T872298722
Ten-High Straight FlushT9622T8622T7622986229762287622
Nine-High Straight Flush985229752296522875228652276522
Eight-High Straight Flush874228642285422764227542265422
Seven-High Straight Flush763227532274322653226432254322
Five-High Straight Flush54A2253A2243A22
Hands with Two Deuces
288Five of a KindC(4,2) x 12 x C(4,3)
1,320Straight FlushC(4,2) x 55 x 4
19,008Four of a KindC(4,2) x C(4,2) x 12 x 44
0Full Housenot possible
3,960FlushC(4,2) x C(12,3) x 4 - 1,320
19,800StraightC(4,2) x 55 x 43 - 1,320
59,400Three of a Kind103,776 - 288 - 1,320 - 19,008 - 3,960 - 19,800
103,776TOTAL

Almost done. Next, I compute the frequencies for hands containingjust a single wild Deuce.

Hands with One Deuce
48Five of a Kind4 x 12
544Straight Flush4 x 34 x 4
8,448Four of a Kind4 x C(4,3) x 12 x 44
9,504Full House4 x C(4,2) x C(4,2) x (12x11/2!)
7,376Flush4 x C(12,4) x 4 - 544
34,272Straight4 x 34 x 44 - 544
253,440Three of a Kind4 x C(4,2) x 12 x (44x40/2!)
0Two Pairnot possible
464,688One Pair4 x C(12,4) x 44 - 544 - 7,376 - 34,272
0High Cardnot possible
778,320TOTAL

Lastly, we handle all the cases where a hand has no wild cards.

Hands with No Deuces
0Five of a Kindnot possible
32Straight Flush8 x 4
528Four of a Kind12 x 44
3,168Full HouseC(4,3) x 12 x C(4,2) x 11
3,136Flush4 x C(12,5) - 32
8,160Straight8 x 45 - 32
42,240Three of a Kind12 x C(4,3) x (44x40/2!)
95,040Two Pair(12 x C(4,2) x 11 x C(4,2))/2! x 40
760,320One Pair12 x C(4,2) x (44 x 40 x 36)/3!
799,680High Card(48 x 44 x 40 x 36 x 32)/5! - 32 - 3,136 - 8,160
1,712,304TOTAL

Okay, that was a lot of work, but we have used raw math to enumerateall the various hand frequencies. The final test was to see if thetotals obtained from my poker code matched the totals obtainedemperically. In other words, if my poker code states that there are672 Five-of-a-Kind hands, then if I add up all the various ways tomake a Five-of-a-Kind using from one to four Deuces, they should beequal.

Breakdown of Five Card Poker Hands
with Deuces Wild
Hand RankNo
Deuces		One
Deuce		Two
Deuces		Three
Deuces		Four
Deuces		SUM
Five of a Kind04828828848672
Straight Flush325441,32065602,552
Four of a Kind5288,44819,0083,568031,552
Full House3,1689,50400012,672
Flush3,1367,3763,9600014,472
Straight8,16034,27219,8000062,232
Three of a Kind42,240253,44059,40000355,080
Two Pair95,040000095,040
One Pair760,320464,6880001,225,008
High Card799,6800000799,680
TOTAL1,712,304778,320103,7764,512482,598,960
At this point, it might be interesting to see how the 'normal'distribution of poker hands changes when we introduce four wildDeuces. As expected, most of the hand count frequencies increase,with the exception of the Two Pair and High Card hands.
Five Card Poker Hands
Nothing WildDeuces WildHand Rank
0672Five of a Kind
402,552Straight Flush
62431,552Four of a Kind
3,74412,672Full House
5,10814,472Flush
10,20062,232Straight
54,912355,080Three of a Kind
123,55295,040Two Pair
1,098,2401,225,008One Pair
1,302,540799,680High Card
2,598,9602,598,960TOTAL

One might be tempted to re-order the poker hands based on thenew frequency counts. If you did so, the Four-of-a-Kind handwould be placed between the Flush and Straight hands, theThree-of-a-Kind and Two Pair hands would swap places, and sowould the One Pair and High Card hands. However, in everyhome game that I've played in that allows wild cards, I havenever seen the hand rankings rearranged based on the 'true'frequencies. In other words, a Flush still loses to a Four-of-a-Kind, even thought it is actually harderto get a Flush than a Four-of-a-Kind when Deuces are wild. There are a number of reasons for keeping the poker handrankings order unchanged. First, every poker player hasalready committed the 'correct' ordering of poker hands to memory. Everyonejust knows that a Four-of-a-Kind is a powerful hand. Nobodywants to be forced to remember another ordering just forwild card games. Plus, some player would inevitably forgetthe new ordering, bet his Four-of-a-Kind heavily, and thenget extremely angry when he loses to a Flush or a Full House.Second, one could always 'cheat' by changing the value ofyour hand. For example, suppose you hold three wild Deucesalong with the Six and Jack of Spades. Logic would tellyou that you have Four Jacks with a Six kicker. However,since Full Houses are supposedly harder to get than Four-of-a-Kinds,you would instead say that you have a Full House, Jacks overSixes. It's sort of a Catch-22. If you rearrange the pokerhand orders, then players will just start calling their handsdifferently to circumvent the new ordering, which in turn willscrew up the frequencies again, which sort of defeats thepurpose of re-ordering the hands in the first place!I guess one could get around this trickery (of a handhaving multiple values) by enforcing a 'rule' that a playerwith wild cards must call his hand as high as possible basedon the 'normal' frequencies, even if that means having a losing hand; but that also would be hard to remember andcause lots of frustration at showdown. Third, one of themain reasons of having wild card games is the chance to gleefullyannounce that you have a Four-of-a-Kind or a Straight Flush.Let's face it, that doesn't happen too often in regular poker.It's great fun to be able to lay down and win with one ofthese 'power' hands, which wouldn't happen as often if we put theFour-of-a-Kind in its 'proper' place. Lastly, consider thegame of Seven Card Stud (nothing wild). Each player at showdownwill have seven cards, of which they each make the best fivecard hand possible. If you calculate the hand frequencies ofall possible C(52,7) combinations, and order them based on theirlikelihood of appearing, you get the exact same order as we didwith just five cards, except that One Pair is easier toget than a High Card hand. It's actually easier to get a pairthan seven crappy cards (which explains why the game Razz isso much fun), but the poker community didn't tryto reverse the hand rankings of those two hands when playingSeven Card Stud. They remained the same. So likewise, even thoughwild cards throw the hand rankings all out of whack, the 'normal'ordering is maintained.

Well, I hope you enjoyed this geeky and math-laden journey intothe world of poker. I doubt if this information will make youa better poker player, and unless you play in a home game, youprobably won't be playing too many games containing wild cards.

Cactus Kev, copyright 2003

Table Of Contents

Do you want to know what beats what in poker? Use the official poker hands rankings chart and seem them from best to worst!

Whether you play live at your local casino or card room, you have your home game going, or you prefer the online action at websites like PokerStars, 888Poker, or partypoker, you need to learn the order of poker hands from best to worse.

Use the list of poker hands below to know what beats what in poker.

Commit this poker hands ranking list to memory today and print it if you need it (there's a button for it at the bottom). Knowing the correct poker hands rank is key to start making winning poker hands.

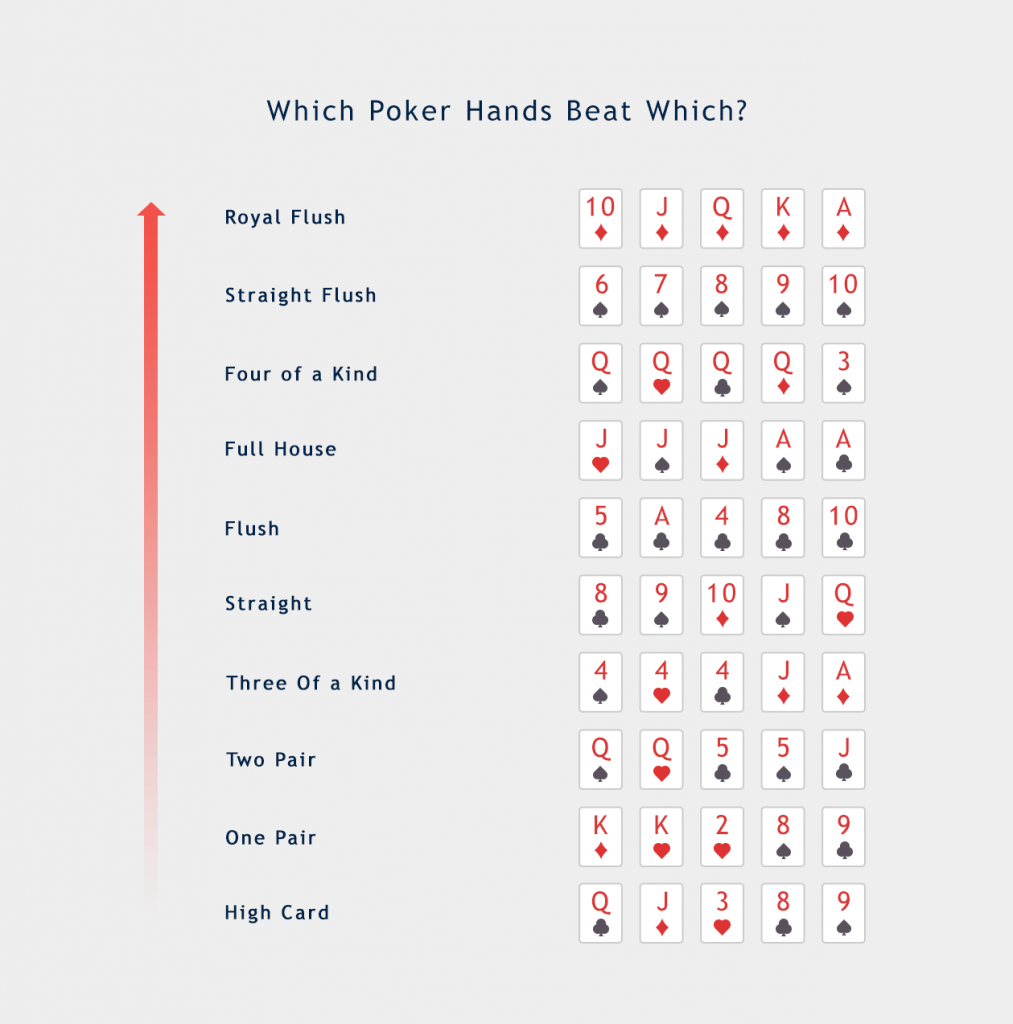
Poker Hands From Best To Worst

Poker Hands From Best To Worst

1. Royal Flush10JQKAThe best possible hand in Texas hold'em is the combination of ten, jack, queen, king, ace, all of the same suit
2. Straight Flush56789Five cards of the same suit in sequential order
3. Four of a kind3333KAny four numerically matching cards
4. Full houseJJJKKCombination of three of a kind and a pair in the same hand
5. Flush2459KFive cards of the same suit, in any order
6. StraightA2345Five cards of any suit, in sequential order
7. Three of a kind77745Any three numerically matching cards
8. Two pair99KK4Two different pairs in the same hand
9. One pair10103QKAny two numerically matching cards
10. High cardK248QThe highest ranked card in your hand with an ace being the highest and two being the lowest
Download as PDF / ImageImage

Not Sure What Beats What in Poker?

Many consider poker less of a gambling game than other casino games. For that to be true, players need to improve their understanding of game play and the strategy required to be a winning player.

The first step toward learning how to play poker is to learn the poker hand rankings.

Most poker players have these rankings memorized, which allows them to think about other things at the table when deciding the best way to play their hands.

The good news is these hand rankings tend to be the same among a wide variety of poker variants, whether it is Texas Hold'em, Omaha, seven-card stud, or other games.

All of those games use the same traditional poker hand rankings that were first developed way back in the 19th century when five-card draw first started to be played.

On this page, you find a complete list of poker hand rankings going from the highest possible hand (the Royal Flush), down to the lowest hand in which there is no pair among the five cards.

Kind

Hand rankings in poker correspond to the likelihood of making such hands.

A royal flush, consisting of the cards ranked ace through ten all being the same suit, is extremely rare — in fact, some players go their entire lives without making a royal flush.

A regular straight flush with any five consecutive cards of the same suit is a little less rare, four of a kind occurs slightly more frequently, and so on.

Notice that a full house is ranked higher than a flush.

That's because a full house comes just a little less frequently than a flush, thereby making it the higher-ranked hand of the two.

Additional readings for beginners:

  • Poker Tips: A collection of tips 'to bring your game from 'meh' to amazing' created to help beginners become better players.
  • Texas Hold'em Strategy: a complete manual to read as soon as you start to remember what beats what in poker.
  • Poker starting hands chart: the only article you need to read to learn how to use your cards to the fullest.

Understanding Winning Poker Hands

Players new to the game of Texas hold'em often struggle, at least at first, with what the best poker hands are.

Once they have read this easy-to-digest guide that will no longer be the case.

The aim of Texas hold'em is to make the best five-card poker hand at showdown.

You can win without having to show your cards if you force someone to fold before the river. Nonetheless, for the purpose of this article, we'll pretend that we've gone to showdown and need to know what beats what in poker.

Winning Poker Hands: What Are The Best Hands In Poker?

First up is the weakest possible holding you can make in poker, a hand that can still win you the pot, although the likelihood of that happening decreases in a pot involving multiple players.

We are of course talking about high card.

As the name suggests, you don't even hold a pair here and instead are using the highest card among the five you are playing.

Example:

You have and the board has come .

Your best five-card hand would be where you would hold queen-high.

Next up is one pair, one of the more common Texas hold'em hands and one that will win you plenty of pots.

Example:

You have and the board comes .

Your five-card hand is — you have a pair of aces. Nice poker hand!

One place higher up on the poker hands chart is two pair.

Example:

You have and the five community cards are .

Your best five-card hand at showdown is or two pair, tens and nines.

One note of warning on this specific poker hand: if you are verbally declaring your hand, try to announce the higher pair first as to help avoid confusion.

Good Poker Hands

Now we're getting into the realm of the best poker hands because once you make three-of-a-kind (sometimes called a set or trips), you are much more likely to win the pot than with any of the previously mentioned hands.

Example:

Your five-card poker hand is — you have three-of-a-kind kings, often a very powerful hand in hold'em.

To beat three-of-a-kind you're going to need at least a straight.

A straight is five consecutive cards where at least one of them is a different suit from the others.

Example:
Should your hand read you would hold a six-high straight.

If someone held a seven-high straight, then that player would win the hand.

There are two straights that have nicknames that are worth remembering.

A wheel is a straight that runs from ace-to-five, and a Broadway straight — the strongest straight — runs from ten-to-ace.

A flush is one of the most powerful Texas hold'em hands because it is only beaten by a handful of others.

Any hand that that has five cards of the same suit is a flush.

Aces are always high when it comes to flushes, which means a hand such as beats .

There are few hands that can beat a flush — one that does is a full house. Also called a 'boat,' a full house is when your five-card hand is made up of three of a kind plus a pair.

Example:

With you have kings full of deuces, while is fives full of queens.

When it comes to full houses, the higher three of a kind determines which hand wins, so in this case 'kings full' would beat 'fives full.'

The Stronger Hands in Poker

The next three holdings are so rare that if you hold them, you can almost guarantee that they are winning poker hands.

Four of a kind is the minimum holding you'll need to beat someone with a full house.

Again, as the name suggests, four of a kind means having four cards of the same rank.

Example:

is four-of-a-kind tens and an extremely powerful holding.

Your only way to beat four of a kind, or 'quads' as they are often called, is to hold either a straight flush or a Royal Flush.

The former is five consecutive cards all of the same suit, so would be an eight-high straight flush and practically unbeatable.

If you manage to make (or the same holding in any of the other three suits), you have a Royal Flush and the only way to lose the hand would be to fold by accident!

Poker Hands Probability

If you are into numbers (most poker players are), you might be wondering about the probability of poker hands.

We said that she platers might go entire lives without ever getting the highest hand in poker but, looking at the numbers, what are the odds of a Royal Flush?

In this section of our complete analysis of the poker hand ranking and what beats what in poker, you get a clear overview of the probability of poker hands.

How to calculate the probability of poker hands?

When you know that there are 52 cards in play and 2,598,960 possible combinations, the calculation is easy.

You just need to divide the number of possibilities to build a specific poker hand by the number of total poker hands.

Let's run a few examples:

What are the odds of a Royal Flush? 0.000,001,539
(4/2,598,960)

What are the odds of a Straight Flush? 0.000,015,39
(40/2,598,960)

Use the table below to calculate the probabilities of all poker hands.

Poker HandNo. WaysProbability
Royal Flush40.000,001,539
Straight Flush400.000,015,39
Four-of-a-Kind6240.000,240,1
Full House3,7440.001,440,58
Flush5,1080.001,965,4
Straight10,2000.003,924,65
Three-of-a-Kind54,9120.021,128,45
Two Pairs123,5520,047,539,02
One Pair1,098,2400,422.569.03

Absolute Value vs. Relative Value of Poker Hands

It should be noted also that while poker hand rankings never change, sometimes circumstances can make a good hand less valuable and a poor hand more valuable.

In other words, when it comes to poker hands there's a difference between absolute value (reflected in the list of poker hands above) and relative value.

For instance, in a game of Texas hold'em, if you have two pair that might seem like a good hand.

But if your opponent keeps betting into you and it's possible he could have a straight or flush, your two pair is no longer looking so good.

Meanwhile, if you have just one pair but your opponent keeps checking to give you a free play at the pot, you might well have the strongest hand and should bet your hand.

The 'absolute' value of your hand may not be great, but in that case the 'relative' value very well could be.

Also worth mentioning is the fact that in some games like razz, deuce-to-seven triple draw, Badugi, and others you might encounter when playing online poker, the hand rankings listed below do not apply.

These hand rankings are for regular or 'high-card' games, not 'lowball' games with alternate hand rankings.

Poker Hand Rankings F.A.Q.

What is the order of poker hands?

As shown in the poker hand rankings chart, the order of poker rankings (from the highest to the lowest) is: Royal Flush, Straight Flush, Four-of-a-Kind, Full House, Flush, Straight, Three-of-a-Kind, Two Pair, One Pair, High Card.

What is the best hand in poker?

The Royal Flush is the best hand in poker. To have a Royal Flush, you need an Ace, a King, a Queen, a Jack, and a 10. All the cards that compose the hand need to be of the same suit.

What beats what in poker?

As you can see in our poker hand rankings chart, the hands in poker follow a clear hierarchy.

In a game of poker, the hand rankings work as follows:

  • a pair beats a high card;
  • a two pair beats a one pair;
  • a three-of-a-kind beats a two pair;
  • a straight beats a three-of-a-kind;
  • a flush beats a straight;
  • a full house beats a flush;
  • a four-of-a-kind beats a full house;
  • a straight flush beats a four-of-a-kind;
  • a Royal Flush beats a straight flush.

The Royal Flush is the best hand in poker, so no one other hands beat this one.

What is a straight in poker?

You have a straight when all the five cards that compose your poker hand are consecutive ones. E.g. 5-6-7-8-9.

If the cards are of the same suit, you have a straight flush, which is a considerably stronger hand compare d to the simple straight.

What beats a straight in poker?

Although many see the straight as a stronger hand, there are many other poker hands that beat it.

The list of hands that beat a straight includes:

  • a flush;
  • a full house;
  • a four-of-a-kind;
  • a straight flush;
  • a Royal Flush.

What beats a flush in poker?

The list of hands that beat a flush includes:

  • a full house;
  • a four-of-a-kind;
  • a straight flush;
  • a Royal Flush.

What beats a full house in poker?

The list of hands that beat a full house includes:

  • a four-of-a-kind;
  • a straight flush;
  • a Royal Flush.

What is the highest suit in poker?

All the suits in poker have the same value. In some games, different suits can be assigned different values.

When that happens, the value is as follow (from the lowest to the highest): clubs, diamonds, hearts, spades. In that case, spades is the highest suit.

How many poker hands are there?

The total number of poker hands in a game of poker is 2,598,960. Since a game of poker uses a 52-card deck of French cards, there are 2,598,960 different possible combinations (aka. poker hands).

What hands to play in poker?

The type of hands to play in a poker game depends on the game you play and other factors like your position in the hand, your stack, and the action at the table.

In a famous poker strategy article, professional player Jonathan Little shared which hands to play in poker and how to play marginal hands.

Can you make three pairs?

Although it is possible to hold a pair in your hand and then have another two pair appear among the five community cards, you can only use a total of five cards to make your poker hand, so you don't win anything for three pairs.

Poker Hands Ranking With 5 Of A Kind

Which is better, a set or trips?

They are both essentially the same hand because they are both three of a kind.

The terminology 'set' is used when you have a pair as your hole cards and then catch another one of those cards on the board.

'Trips' is when there is a pair on the board and you have another of those cards as one of your hole cards.

Sets are easier to disguise than trips so many consider them to be a better hand, although they both rank the same.

What is a chopped or split pot?

Poker Hands With 5 Of A Kind

If you and an opponent have the same five-card poker hand, then the pot is divided equally between you.

Say you have and your opponent has , and the board comes .

You both would be playing the same five-card hands in terms of their value (A-J-T-8-3), and so would split the pot.

Poker Hands 5 Of A Kind

If there is four of a kind on the board, who wins?

Because the aim is to make a five-card poker hand, whoever has the highest fifth card in this case wins.

If the board reads and you have in your hand and your opponent has , then you win because you hand is 7-7-7-7-A and your opponent's is 7-7-7-7-K.

You would also win even if your opponent holding was in this example.

Are the suits ranked in Texas hold'em?

No, they are not. Some poker variants have different ranks for suits, but hold'em is not one of them.

Why did my 4-4-4-T-T lose to my opponent's 7-7-7-8-8?

As mentioned earlier, it is the three-of-a-kind element of a full house that dictates the winner.

If you're new to the game and want a reference of all of Texas hold'em hands, you can keep this page open or you could always download and print our poker hands ranking chart and keep it next to you while you're playing poker.

Useful Poker Tools

  • Poker Odds Calculator: Add your cards to the calculator to discover your chances to win the hand.
  • How to use PokerStars Tools to Your Advantage: As a beginner, this article can save your life! Let us show you how you can use all the tools available on the PokerStars client to become an outstanding poker player!

Must Have Rooms

Home to the biggest tournaments online, these rooms also have the largest player base, great bonuses, tons of action and the best software. If you don't have accounts here, you are missing out on the best that online poker has to offer.

PartyPokerplatinum

Poker Hands Chart With 5 Of A Kind

Up to $30 of Free Play

Poker Hand 5 Of A Kind

RATING

9.9 ★

Key features

  • Excellent mobile poker games
  • Lots of free and real-money action
  • One of the most trusted brands in online gaming